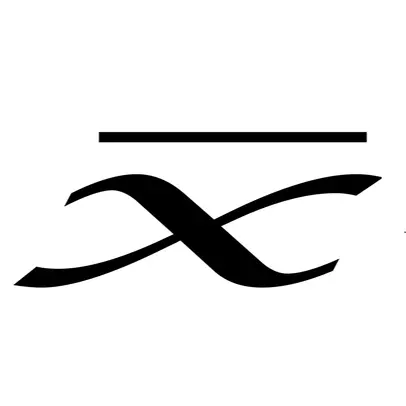Tabla de frecuencias

Calculadora de frecuencias

Una aplicación o página web para crear una tabla de frecuencias de forma automática

Xi fi Fi hi % Hi

Otras estadísticas:

¿Que son las tablas de frecuencias?

Las tablas de frecuencias son aquellas tablas en las que se reflejan una serie de datos y sus respectivos cálculos.

Dependiendo de los cálculos que vallamos a realizar podemos considerar que es una Tabla de frecuencias para niños, una tabla de frecuencias para primaria, o incluso podemos adaptarla para parecerse a una tabla de frecuencias para 3º de la ESO.

Calculadora cientifica básica Casio

¿Con que hago una tabla de frecuencias?

Una tabla de frecuencias se puede realizar o desarrollar de forma clásica a boli y papel, en el ordenador en un Excel o en tabladefrecuencias.com

Se puede escribir con papel y boli y realizando las cuentas con la calculadora o incluso también se pueden hacer con boli y papel

Otra forma es construir la tabla de frecuencias en un Excel e ir introduciendo los respectivos datos y fórmulas en cada casilla como se explica en a continuación.

Y la forma más rápida es hacerlo de forma online en esta calculadora de tabla de frecuencias donde nada más hace falta introducir una serie de números en el formulario de la parte superior de la página para que se realicen los cálculos automáticamante.

¿Porque son importantes las tablas de frecuencias?

La tabla de frecuencias es una herramienta muy útil que nos ayuda a saber todo sobre una serie de números y así tomar decisiones sobre cuál de estos es el más adecuado para cada circunstancia.

Una vez que ya sabemos para qué sirve la tabla de frecuencias y cómo funciona podríamos aplicarla al mundo de las finanzas, estadísticas, marketing o salud mental.

¿Como hacer una tabla de frecuencias?

A continuación te muestro como elaborar una tabla de frecuencias:

  1. Introducir la secuencia de números a analizar y ordenarlos de menor a mayor.
  2. Calcular la frecuencia absoluta.
  3. Calcular la frecuencia acumulada.
  4. Calcular la frecuencia relativa.
  5. Calcular el porcentaje.
  6. Calcular la frecuencia relativa acumulada.
como calcular la frecuencia absoluta

Como calcular la frecuencia absoluta

La frecuencia absoluta es el número de veces que se repite el número a analizar.

Su símbolo es: fi

Ejemplo de cómo calcular la frecuencia absoluta:

  • Serie de números: 8;5;1;7;5;3;9
  • Número a analizar: 7
  • Frecuencia absoluta: 1
como se calcula la frecuencia absoluta acumulada

Como calcular la frecuencia absoluta acumulada

La frecuencia absoluta acumulada de un número es la suma de la frecuencia absoluta y la frecuencia absoluta acumulada del anterior número.

Como el primer número no tiene ninguno anterior su frecuencia absoluta acumulada es la misma que su frecuencia absoluta.

La frecuencia absoluta acumulada de todos los número o frecuencia absoluta acumulada final es la frecuencia absoluta acumulada del último número.

La frecuencia absoluta acumulada final coincide con el número de datos, repetidos o no, de la serie.

Su símbolo es: Fi

Esta es la fórmula de la frecuencia absoluta acumulada: Fi-1+fi

Ejemplo de cómo sacar la frecuencia absoluta acumulada del primer número:

  • Serie de números: 4;7;8;6;7;9;4
  • Número a analizar: 4
  • Frecuencia absoluta: 2
  • Frecuencia absoluta acumulada: 2

Ejemplo de cómo sacar la frecuencia absoluta acumulada de otro número:

  • Serie de números: 4;7;8;6;7;9;4
  • Número a analizar: 7
  • Número anterior: 6
  • Frecuencia absoluta acumulada del 6: 3
  • Frecuencia absoluta: 2
  • Frecuencia absoluta acumulada: 5

Ejemplo de cómo sacar la frecuencia absoluta acumulada del último número:

  • Serie de números: 4;7;8;6;7;9;4
  • Número a analizar: 9
  • Frecuencia absoluta: 1
  • Frecuencia absoluta acumulada: 7
como calcular frecuencia relativa

Como calcular la frecuencia relativa

La frecuencia relativa es el resultado de la división de la frecuencia absoluta entre la frecuencia absoluta acumulada final o de todos los números.

Su símbolo es: hi

Esta es la fórmula de la frecuencia relativa: fi/F

Ejemplo de cómo sacar la frecuencia relativa:

  • Serie de números: 4;8;7;6;4;0;9;5;4;6
  • Número a analizar: 4
  • Frecuencia absoluta: 3
  • Frecuencia absoluta acumulada: 4
  • Frecuencia relativa: 0.10
como calcular el porcentaje

¿Cómo sacar el porcentaje?

El porcentaje es el producto de multiplicar la frecuencia relativa por 100.

Su símbolo es: %

Esta es la fórmula del porcentaje: fi*100

Ejemplo de cómo sacar el porcentaje:

  • Serie de números: 1;2;5;9;7;6;5
  • Número a analizar: 5
  • Frecuencia relativa: 0.29
  • Porcentaje: 29%
frecuencia relativa acumulada

¿Como calcular la frecuencia relativa acumulada?

La frecuencia relativa acumulada de un número es la suma de la frecuencia relativa y la frecuencia relativa acumulada del anterior número.

Como el primer número no tiene ninguno anterior su frecuencia relativa acumulada es la misma que su frecuencia relativa.

La frecuencia relativa acumulada de todos los número o frecuencia relativa acumulada final es la frecuencia relativa acumulada del último número, si todo ha ido bien, 1.

Su símbolo es: Hi

Esta es la fórmula de la frecuencia relativa acumulada: Hi-1+hi

Ejemplo de cómo sacar la frecuencia relativa acumulada del primer número:

  • Serie de números: 9;5;7;6;5;3;4
  • Número a analizar: 3
  • Frecuencia relativa: 0.14
  • Frecuencia relativa acumulada: 0.14

Ejemplo de cómo sacar la frecuencia relativa acumulada de otro número:

  • Serie de números: 9;5;7;6;5;3;4
  • Número a analizar: 5
  • Frecuencia relativa: 0.29
  • Número anterior: 4
  • Frecuencia relativa acumulada del 4: 0.29
  • Frecuencia relativa acumulada del 5: 0.57

Ejemplo de cómo sacar la frecuencia relativa acumulada del último número:

  • Serie de números: 9;5;7;6;5;3;4
  • Número a analizar: 9
  • Número anterior: 7
  • Frecuencia relativa acumulada del 7: 0.86
  • Frecuencia relativa: 0.14
  • Frecuencia relativa acumulada: 1
como se calcula la moda en una tabla de frecuencias

¿Como calcular la moda de una serie de números?

La moda de una serie de números es el número que más veces se repite.

También podemos utilizar la frecuencia absoluta para saber cuale es el número qe más se repite; La moda será igual al número que la teng más alta

Su simbolo es: x̂

Ejemplo de como sacar la moda:

  • Serie de números: 4;7;8;4;5;1
  • Como el número 4 es el número que más veces(2) se repite es la moda
  • Moda: 4
como se calcula la media en una tabla de frecuencias

¿Como calcular la media de una serie de números?

La media de una serie de numeros es el promedio que se obtiene de la suma de todos los números entre el número de ellos.

Su simbolo es: x-

Ejemplo de como sacar la media:

  • Serie de números: 3;4;2;0;7;8;6;2
  • Suma de todos los números: 3+4+2+0+7+8+6+2=32
  • Cantidad total de números: 8
  • Media: 32/8=4
como se calcula la mediana en una tabla de frecuencias

¿Como calcular la mediana de una serie de números?

La mediana de una serie de números es el valor del número que queda en medio de la serie de números una vez que esta ya ha sido ordenada.

Si la cantidad total de números es par la mediana será la media de los dos números que queden entre medio.

Su símbolo es: x~ σ²

Esta es la fórmula de la mediana para una serie con un número impar de valores: x~=x(n+1)/2

Esta es la fórmula de la mediana para una serie con un número par de valores:x~=0.5(xn/2+xn/2+1)

Ejemplo de como sacar la mediana de una serie de números impar:

  • Serie de números: 3;8;5;4;7;3;7
  • Serie ordenada: 3;3;4;5;7;7;8
  • Número total de valores: 7
  • Mediana: 5
  • Aplicando la fórmula: x~=x(7+1)/2=x8/2=x4=5

Ejemplo de como sacar la mediana de una serie de números par:

  • Serie de números: 12;18;56;20;61;15;43;18
  • Serie ordenada: 12;15;18;18;20;43;56;61
  • Número total de valores: 8
  • Números de entremedio: 18;20
  • Media de números de entremedio:19
  • Aplicando la fórmula:
  • x~=0.5(x8/2+x8/2+1);
  • x~=0.5(x4+x4+1);
  • x~=0.5(x4+x5);
  • x~=0.5(18+20);
  • x~=0.5*38;
  • x~=19;
como calcular la varianza

¿Como calcular la varianza?

La varianza de una serie de números es la media de la desviación respecto a la media de estos.

Su símbolo es: σ²

Se calcula restando el cuadrado de la media a la división de la sumatoria de cada número al cuadrado por su frecuencia absoluta entre la cantiad total de números

Esta es la fórmula para calcular la varianza: σ²=(∑(xi2fi2))/N-x-

  • Serie de números: 2;3;2;4;4;3;8;7;3
  • Serie ordenada:2;2;3;3;3;4;4;7;8
  • Números: 2;3;4;7;8
  • Núnmeros al cuadrado: 4;9;49;64
  • Frecuencia absoluta: 2;3;2;1;1
  • Cantidad total de números o frecuencia absoluta acumulada final: 9
  • Media: 4
  • Media al cuadrado: 16
  • Varianza: 4
como calcular la desviación típica o variación estándar

¿Cómo calcular desviación típica?

La desviación típica o variación estándar es otro valor que indica la distancia entre los diferentes números de la serie.

Para calcular la desviación típica o variación estándar simplemente debemos de hallar la raíz cuadrada de la varianza.

  • Serie de números: 2;3;2;4;4;3;8;7;3
  • Varianza: 4
  • Desviación típica: 2

¿Como calcular el coeficiente de variación?

El coeficiente de variación es el último medidor de diferencias entre los diferentes valores y la media de una serie de números.

El coeficiente de variación se calcula dividiendo la desviación típica entre la media.

  • Serie de números: 2;3;2;4;4;3;8;7;3
  • Deviación típica: 2
  • Media: 4
  • Coeficiente de variación: 0.5
tablas de frecuencias excel

¿Como hacer una tabla de frecuencias en Excel?

Suponemos que tenemos esta serie de datos:9;4;5;8;7;9;5

  1. Abrimos un nuevo documento en blanco en Excel
  2. Rellenamos la fila de los encabezados de la siguiente manera:
    • A1: Xi
    • B1:fi
    • C1:Fi
    • D1:hi
    • E1:%
    • F1:Hi
  3. Rellenamos la columna de los números(Xi) con cada nuevo número ordenadamente de menor a mayor:
    • A2: 4
    • A3: 5
    • A4: 7
    • A5: 8
    • A6: 9
  4. Rellenamos la columna de la frecuencia absoluta(fi) con el número de veces que se repite cada número de la izquierda:
    • B2: 1
    • B3: 2
    • B4: 1
    • B5: 1
    • B6: 2
  5. Rellenamos la primera celda de la columna correspondiente a la frecuencia absoluta acumulada (Fi) con el mismo valor que la frecuencia absoluta:
    • C2: 1
  6. Rellenamos la segunda celda de la columna correspondiente a la frecuencia absoluta acumulada(Fi):
      C3: =C2+B3
  7. Arrastramos la fórmula desde la esquina inferior derecha de la celda C3 hasta la última fila.
  8. Rellenamos la primera celda de la columna correspondiente a la frecuencia relativa(fi):
    • D2: =B2/C$5
  9. Arrastramos la fórmula desde la esquina inferior derecha de la celda D2 hasta la última fila.
  10. Rellenamos la primera celda de la columna correspondiente al porcentaje:
      11. E2: D2*100
  11. Arrastramos la fórmula desde la esquina inferior derecha de la celda E1 hasta la última fila.
  12. Rellenamos la primera celda de la columna correspondiente a la frecuencia relativa acumulada(Fi):
    • F2: =D2
  13. Rellenamos la segunda celda de la columna correspondiente a la frecuencia relativa acumulada(Fi):
    • F3: =F2+D3
  14. Arrastramos la fórmula desde la esquina inferior derecha de la celda F3 hasta la última fila.
  15. Moda: Utilizamos la función moda() que nos proporciona Excel y como parámetro pasamos la serie de números.
  16. Media: Utilizamos la función suma(), como parámetro pasamos la serie de números, y la dividimos entre el número resultante de la función contar(), a esta también le pasamos como parámetro la serie de números.
    • R4=promedio(I1:P1)
  17. Mediana: Utilizamos la función mediana() que nos propociona Excel y como parámetro pasamos la serie de números.
    • R9=mediana(I1:P1)
  18. Varianza: nombramos la casilla Q10 como varianza
  19. Nombramos la casilla G3 como Xi2fi
  20. Escribimos el siguiente valor a la casilla H3: A2*A2*B2
  21. Arrastramos desde la esquina izquierda inferior hasta la última casilla H7
  22. Añadimos el siguiente valor a la casilla H8: =suma(H3:H7)
  23. Añadimos el siguiente valor a la casilla R10: =(H8/C6)-(R4*R4)
  24. Titulamos a la casilla Q11 como desviación típica
  25. Le damos el siguientre valor a la casilla R11: =RAIZ(R10)
  26. Asignamos el nombre de Coeficiente de variacíon a la casilla Q12
  27. Escribimos la siguiente fórmula para la casilla R12: R11/R4

Otro ejemplo con otra serie de números

Serie de números: 5;7;9;5;1;9;0

Números: 0,1,5,7,9

Frecuencia absoluta del 0: 1

Frecuencia absoluta del 1: 1

Frecuencia absoluta del 5: 2

Frecuencia absoluta del 7: 1

Frecuencia absoluta del 9: 2


Frecuencia absoluta acumulada del 0: 1

Frecuencia absoluta acumulada del 1: 2

Frecuencia absoluta acumulada del 5: 4

Frecuencia absoluta acumulada del 7: 5

Frecuencia absoluta acumulada del 9: 7


Frecuencia relativa del 0: 0.14

Frecuencia relativa del 1: 0.14

Frecuencia relativa del 5: 0.29

Frecuencia relativa del 7: 0.14

Frecuencia relativa del 9: 0.29


Porcentaje del 0: 14%

Porcentaje del 1: 14%

Porcentaje del 5: 29%

Porcentaje del 7: 14%

Porcentaje del 9: 29%


Frecuencia relativa acumulada del 0: 0.14

Frecuencia relativa acumulada del 1: 0.29

Frecuencia relativa acumulada del 5: 0.57

Frecuencia relativa acumulada del 7: 0.71

Frecuencia relativa acumulada del 9: 1


Moda: 3

Media: 4,13

Mediana 5

Varianza: 10,98

Desviación típica: 3,31

Coeficiente de varianza: 0,64

Tu donativo PayPal aquí

Apoya a Gonzalo Bustamante

Si esta aplicación web le ha servido de ayuda, puede dejar un donativo para seguir mejorándola o pinchar sobre el anuncio para seguir mejorandola.

Otras lecturas recomendadas

Lo que uno siempre puede hacer para adquirir más conocimientos es buscar en el mejor buscador posible y empezar a navegar y aquirir conocimientos.


Por otra parte, puedes usar el SPSS para cuantificar la realidad y disponer de los elementos que nos permitan su análisis. Los trabajos de estadística son útiles por si hay que recoger, analizar e interpretar datos numéricos.


Además, contamos con el apoyo de una empresa que ofrece trabajos de estadística para ayudar a otros profesionales a tomar decisiones informadas y crear políticas de empresa.

COMENTARIOS

Comentarios: 8

Autor: Lira: Fecha: 2022-03-09

Excelente página, calcula los datos correctamente. Seria genial si agregaras más cosas acerca del tema. ¡Saludos!


Responder






Respuestas: 3

Autor: Administrador: Fecha: 2022-04-12

Gracias por tu comentario. Que más cosas te gustaría que agregase?Un saludo.

Respuesta

Autor: La barrera: Fecha: 2022-06-01

Ya te digo

Respuesta

Autor: Administrador: Fecha: 2022-06-01

Pronto habrá un diseño más atractivo y compatible con el móvil para poder implementar nuevas funciones, se aceptan sugerencias.

Respuesta
3

Autor: Antonio: Fecha: 2022-11-27

Excelente página, sería increible que implementaces el algoritmo para las tablas de frecuencia con datos agrupados, un saludo :)


Responder






Respuestas: 1

Autor: Administrador: Fecha: 2022-11-27

Gracias por tu comentario Antonio, Me alegra saber que te halla gustado mi página, La verdad que una de las tareas en la que estoy trabajando actualmente es la página de la tabla de frecuencias de datos agrupados, ¿quieres que te avise cuando la publique? Un saludo

Respuesta
5

Autor: Adriana: Fecha: 2023-06-01

excelente tu pagina web. hace el calculo 100 % efectivo. ningun margen de error te felicito por facilitarnos esta herramienta.


Responder






3

Autor: Karla Martin: Fecha: 2024-03-10

Karla Martin


Responder






1

Autor: Andrés: Fecha: 2024-05-15

Muy útil la herramienta la verdad, aunque un poco diferente el formato al que me están enseñando en mi institución


Responder






Respuestas: 1

Autor: Administrador: Fecha: 2024-05-16

Gracias por el apoyo. Que formato le están enseñando en su institución? Podría crear una nueva página con ese formato.

Respuesta
3

Autor: edison: Fecha: 2024-07-07

interesante Estoy intentando hacer una SL en el sector turismo y me gustaria añadir esta ruleta para ofrecer un premio de un espectaculo.Si uso la ruleta para asignar dicho premio como puedo hacer para que se repita siempre ojo no quiero decir de hacer trampas estoy diciendo que cuando las personas toquen la ruleta para saber quien es el ganador salga siempre la misma porque el premio ya esta adjudicado y no salga una distinta cada vez que se mira no se si me he explicado supongo que tendra que ver con el tema de las frecuencias que parece algo complicado Saludos


Responder






Respuestas: 1

Autor: Administrador: Fecha: 2024-07-08

A que ruleta te refieres?

Respuesta

Autor: Mr.ManitosRapidas : Fecha: 2024-07-14

Excelente pagina, aunque me encantaría que agreguen las medidas de posesión como lo son cuartiles, deciles y percentiles


Responder






Respuestas: 1

Autor: Administrador: Fecha: 2024-07-16

Gracias por tu comentario y sugerencia, lo tendré en cuenta.

Respuesta

Autor: Chocokrak: Fecha: 2024-08-08

Me parecio muy util , una mejora que daria seria que se le pueda tambien hacer graficos


Responder






1